図2.1に永久磁石同期電動機の等価回路を示します。ここで、u,v,w相の各巻線の電気磁気的特性は同一であり、電流、磁束の高調波成分は無視できると仮定します。また、磁気回路の飽和特性などの非線形特性や、軸間磁束の干渉、損失である鉄損はそれぞれ無視できると仮定します。
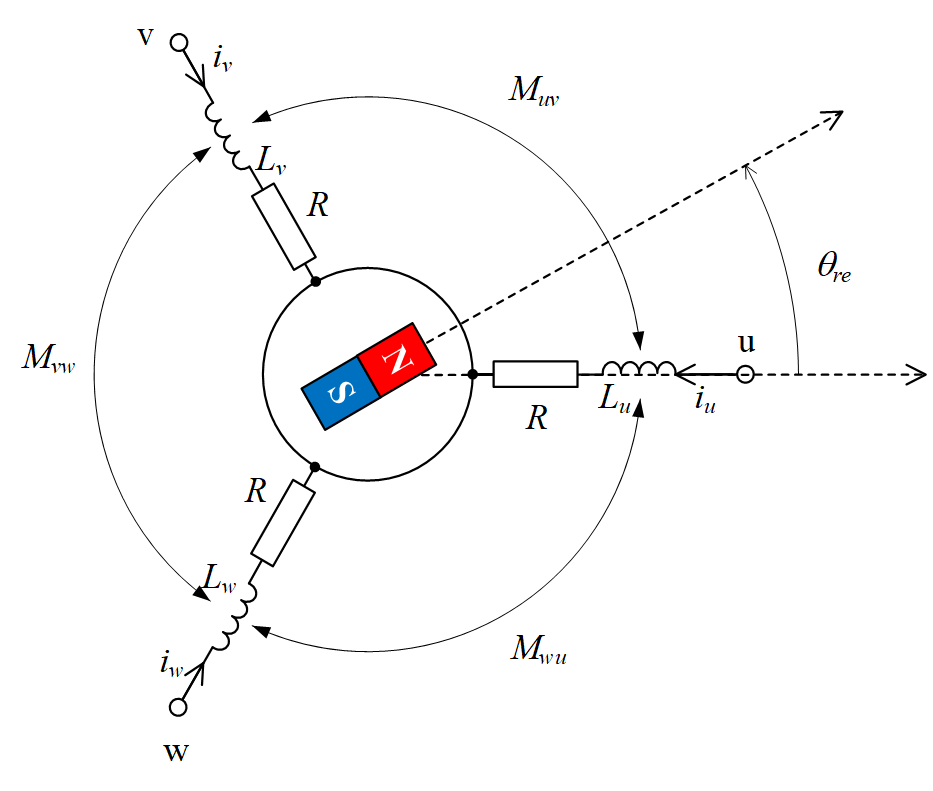
モータの電圧方程式は巻線の電圧降下と誘導起電力から以下の式で求めることができます。
$$
\begin{equation}
\large
\left[ \begin{matrix}
{{v}_{u}} \\
{{v}_{v}} \\
{{v}_{w}} \\
\end{matrix} \right]=R\left[ \begin{matrix}
{{i}_{u}} \\
{{i}_{v}} \\
{{i}_{w}} \\
\end{matrix} \right]+p\left[ \begin{matrix}
{{{{\psi }’}}_{u}} \\
{{{{\psi }’}}_{v}} \\
{{{{\psi }’}}_{w}} \\
\end{matrix} \right] \tag{2.1}
\end{equation}
$$
各相の鎖交磁束は、巻線電流による磁束と永久磁石による磁束からなります。モータ軸を一定速度駆動させたときの無負荷誘導起電力(モータ端子を開放した状態の起電力)が正弦波と仮定すると、磁束を以下の式で表すことができます。
$$
\begin{equation}
\large
\left[ \begin{matrix}
{{{{\psi }’}}_{u}} \\
{{{{\psi }’}}_{v}} \\
{{{{\psi }’}}_{w}} \\
\end{matrix} \right]=\left[ \begin{matrix}
{{L}_{u}} & {{M}_{uv}} & {{M}_{uw}} \\
{{M}_{vu}} & {{L}_{v}} & {{M}_{vw}} \\
{{M}_{wu}} & {{M}_{wv}} & {{L}_{w}} \\
\end{matrix} \right]\left[ \begin{matrix}
{{i}_{u}} \\
{{i}_{v}} \\
{{i}_{w}} \\
\end{matrix} \right]+\left[ \begin{matrix}
{\psi }’\cos {{\theta }_{re}} \\
{\psi }’\cos \left( {{\theta }_{re}}-\frac{2}{3}\pi \right) \\
{\psi }’\cos \left( {{\theta }_{re}}+\frac{2}{3}\pi \right) \\
\end{matrix} \right] \tag{2.2}
\end{equation}
$$
ここで、\(\psi\)’は一相あたりの永久磁石による電機子鎖交磁束の最大値です。各相の鎖交磁束を電圧方程式に代入することで以下の式を得ます。
$$
\begin{equation}
\large
\left[ \begin{matrix}
{{v}_{u}} \\
{{v}_{v}} \\
{{v}_{w}} \\
\end{matrix} \right]=\left[ \begin{matrix}
R+p{{L}_{u}} & p{{M}_{uv}} & p{{M}_{uw}} \\
p{{M}_{vu}} & R+p{{L}_{v}} & p{{M}_{vw}} \\
p{{M}_{wu}} & p{{M}_{wv}} & R+p{{L}_{w}} \\
\end{matrix} \right]\left[ \begin{matrix}
{{i}_{u}} \\
{{i}_{v}} \\
{{i}_{w}} \\
\end{matrix} \right]+\left[ \begin{matrix}
-{{\omega }_{re}}{\psi }’\sin {{\theta }_{re}} \\
-{{\omega }_{re}}{\psi }’\sin \left( {{\theta }_{re}}-\frac{2}{3}\pi \right) \\
-{{\omega }_{re}}{\psi }’\sin \left( {{\theta }_{re}}+\frac{2}{3}\pi \right) \\
\end{matrix} \right] \tag{2.3}
\end{equation}
$$
$$
\begin{equation}
\large
\left[ {{v}_{uvw}} \right]=R\left[ {{i}_{uvw}} \right]+p\left[ {{L}_{uvw}} \right]\left[ {{i}_{uvw}} \right]+\left[ {{e}_{uvw}} \right] \label{3p-PMSM-Mathematical-Model}\tag{2.4}
\end{equation}
$$
(\ref{3p-PMSM-Mathematical-Model})式の各項はそれぞれ以下の通りです。
$$
\begin{align}
& \large\left[ {{v}_{uvw}} \right]={{\left[ \begin{matrix}
{{v}_{u}} & {{v}_{v}} & {{v}_{w}} \\
\end{matrix} \right]}^{T}} \tag{\ref{3p-PMSM-Mathematical-Model}-a}\\
& \large\left[ {{i}_{uvw}} \right]={{\left[ \begin{matrix}
{{i}_{u}} & {{i}_{v}} & {{i}_{w}} \\
\end{matrix} \right]}^{T}} \tag{\ref{3p-PMSM-Mathematical-Model}-b}\\
& \large\left[ {{L}_{uvw}} \right]=\left[ \begin{matrix}
{{L}_{u}} & {{M}_{uv}} & {{M}_{uw}} \\
{{M}_{vu}} & {{L}_{v}} & {{M}_{vw}} \\
{{M}_{wu}} & {{M}_{wv}} & {{L}_{w}} \\
\end{matrix} \right] \tag{\ref{3p-PMSM-Mathematical-Model}-c}\\
& \large\left[ {{e}_{uvw}} \right]={{\left[ \begin{matrix}
-{{\omega }_{re}}{\psi }’\sin {{\theta }_{re}} & -{{\omega }_{re}}{\psi }’\sin \left( {{\theta }_{re}}-\frac{2}{3}\pi \right) & -{{\omega }_{re}}{\psi }’\sin \left( {{\theta }_{re}}+\frac{2}{3}\pi \right) \\
\end{matrix} \right]}^{T}} \tag{\ref{3p-PMSM-Mathematical-Model}-d}\\
\end{align}
$$
