図3.1に三相静止座標系とd-q座標系の関係を示します。ここでは、d 軸を永久磁石磁束の方向と一致させ、d軸より90度進んだ軸をq軸と定義します。
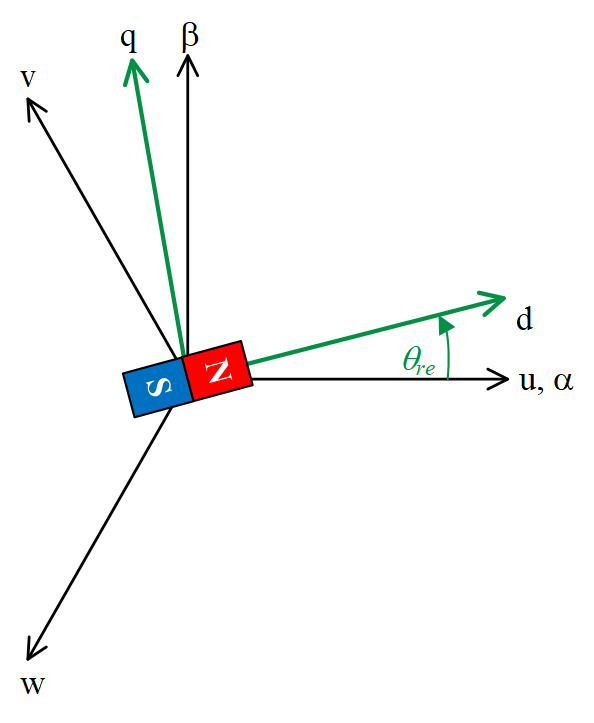
三相静止座標系からd-q座標系への変換は以下の式を用いて回転座標変換することでできます。
$$
\begin{equation}
\large
\left[ C \right]=K\left[ \begin{matrix}
\cos {{\theta }_{re}} & \cos \left( {{\theta }_{re}}-\frac{2}{3}\pi \right) & \cos \left( {{\theta }_{re}}+\frac{2}{3}\pi \right) \\
-\sin {{\theta }_{re}} & -\sin \left( {{\theta }_{re}}-\frac{2}{3}\pi \right) & -\sin \left( {{\theta }_{re}}+\frac{2}{3}\pi \right) \\
\end{matrix} \right] \label{三相静止座標系からd-q座標系への変換}\tag{3.1}
\end{equation}
$$
ここで、\(K\)は座標変換係数です。座標変換には絶対変換と相対変換があり、絶対変換は変換前後の電力が不変、相対変換は変換前後の振幅が不変といった特徴があります。絶対変換の座標変換係数\(K_1\)と相対変換の座標変換係数\(K_2\)はそれぞれ以下の通りです。
$$
\begin{align}
& \large K_1 = \sqrt{\frac{2}{3}} \tag{\ref{三相静止座標系からd-q座標系への変換}-a}\\
& \large K_2 = {\frac{2}{3}} \tag{\ref{三相静止座標系からd-q座標系への変換}-b}\\
\end{align}
$$
回転座標変換行列を三相電圧方程式の左からかけることで座標変換を行います。座標変換を行い、d-q座標数学モデルを導出すると以下の式となります。
$$
\begin{equation}
\large
\left[ \begin{matrix}
{{v}_{d}} \\
{{v}_{q}} \\
\end{matrix} \right]=\left[ \begin{matrix}
R+p{{L}_{d}} & -{{\omega }_{re}}{{L}_{q}} \\
{{\omega }_{re}}{{L}_{d}} & R+p{{L}_{q}} \\
\end{matrix} \right]\left[ \begin{matrix}
{{i}_{d}} \\
{{i}_{q}} \\
\end{matrix} \right]+\left[ \begin{matrix}
0 \\
{{\omega }_{re}}\psi \\
\end{matrix} \right] \tag{3.2}
\end{equation}
$$
PMSMの電圧方程式を状態方程式で表すと以下の式となります。
$$
\begin{equation}
\large
\frac{d}{dt}\left[ \begin{matrix}
{{i}_{d}} \\
{{i}_{q}} \\
\end{matrix} \right]=\left[ \begin{matrix}
-\frac{R}{{{L}_{d}}} & {{\omega }_{re}}\frac{{{L}_{q}}}{{{L}_{d}}} \\
-{{\omega }_{re}}\frac{{{L}_{d}}}{{{L}_{q}}} & -\frac{R}{{{L}_{q}}} \\
\end{matrix} \right]\left[ \begin{matrix}
{{i}_{d}} \\
{{i}_{q}} \\
\end{matrix} \right]+\left[ \begin{matrix}
\frac{{{v}_{d}}}{{{L}_{d}}} \\
\frac{{{v}_{q}}}{{{L}_{q}}} \\
\end{matrix} \right]+\left[ \begin{matrix}
0 \\
-\frac{{{\omega }_{re}}\psi }{{{L}_{q}}} \\
\end{matrix} \right] \tag{3.3}
\end{equation}
$$
電圧型PWMインバータでモータを制御する場合、モータに電圧を入力して電流を制御することになります。状態方程式として表すことで、入力変数である電圧と制御する状態量である電流の関係を理解しやすくなります。
